Open statistical ensemble

Statistical mechanics

Thermodynamics · Kinetic theory
Particle Statistics Spin-Statistics Theorem Identical Particles Maxwell–Boltzmann Bose–Einstein · Fermi–Dirac Parastatistics · Anyonic Statistics Braid Statistics
Ensembles Microcanonical · Canonical Grand canonical Isothermal–isobaric Isoenthalpic–isobaric Open statistical
Models Debye · Einstein · Ising
Potentials Internal energy · Enthalpy Helmholtz free energy Gibbs free energy Grand potential / Landau free energy
Scientists Maxwell · Gibbs · Boltzmann

Open statistical ensemble (OSE) corresponds to a physical system, which exchanges energy with the environment, being with it in thermal equilibrium, exchanges particles with the environment for a given chemical potential and correctly takes into account the surface terms.

The expression for the partition function of the ensemble is similar to the partition function of the grand canonical ensemble (GCE), with the replacement of the Boltzmann factor in terms of the series on the correlation functions of special form.

The coefficient of surface tension, included in the partition function corresponds to the interface of fluid and hard solid, due to the strict respect of probability and potential limitations.

Unlike the GCE, for OSE average number of particles in a given volume is strictly coincides with the volume term. Also in contrast to the GCE, the correlation functions of the OSE strictly satisfy the requirement of translational invariance.

The expression for the general term of the distribution has the form

$p^v_m = \frac{z^m}{m! \Upsilon_v} \sum_{t=0}^\infty \frac{z^t}{t!} \int \left [ \prod_{i = 1}^m \prod_{j = m%2B1}^{m%2Bt}\psi^v_i\chi^v_j \right ] {\mathcal B}^{(m,t)}_{1...m%2Bt} d\boldsymbol{r}_1...d\boldsymbol{r}_{m%2Bt},$

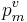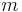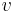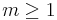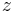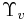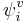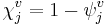where $p^v_m$ is the probability to find $~m$ particles in volume $~v$ , $~m \geq 1$ , $~z$ is activity, $~\Upsilon_v$ - OSE partition function. $~\psi^v_i$ and $~\chi^v_j = 1 - \psi^v_j$ - characteristic functions, equal to unity inside and outside the system, respectively, and 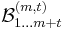$~{\mathcal B}^{(m,t)}_{1...m%2Bt}$ - partial localization factors, generalize the notions of the Boltzmann and Ursell factors and contain them as extreme cases.

The first term of the series corresponds to the distribution of the GCE with the accuracy up to normalizing factors - partition functions.

Summing the series we obtain the expression

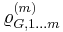$p^v_m = \frac{1}{m! \Upsilon_v} \int \left [ \prod_{i = 1}^m \psi^v_i \right ] \varrho^{(m)}_{G,1...m}(\chi^v) d\boldsymbol{r}_1...d\boldsymbol{r}_m,$

where $~\varrho^{(m)}_{G,1...m}$ - correlation function, depending on 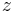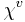$~z$ , $~\chi^v$ and expressed through a series of 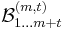$~{\mathcal B}^{(m,t)}_{1...m%2Bt}$ . The last expression is equivalent to the GCE distribution with the replacement

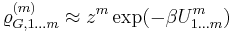
$\varrho^{(m)}_{G,1...m} \approx z^m \exp(-\beta U^{m}_{1...m})$

and corresponding renormalization, where 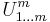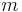$~U^{m}_{1...m}$ - $~m$ -particle interaction potential, 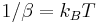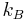$~1/\beta = k_B T$ , $~k_B$ - Boltzmann constant, 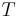$~T$ - temperature. This expression shows that the GCE is a low-density approximation of the OSE.

For the partition function of the OSE, we have the expression

$\Upsilon_v = \exp { \sum_{t=1}^\infty \frac{z^t}{t!} \int \left [1 - \prod_{i = 1}^{t} \chi^v_i \right ] {\mathcal U}^{(t)}_{1...t} d\boldsymbol{r}_1...d\boldsymbol{r}_t },$

unlike the partition function of GCE

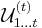$\Xi_v = \exp { \sum_{t=1}^\infty \frac{z^t}{t!} \int \left [ \prod_{i = 1}^{t} \psi^v_i \right ] {\mathcal U}^{(t)}_{1...t} d\boldsymbol{r}_1...d\boldsymbol{r}_t },$

where $~{\mathcal U}^{(t)}_{1...t}$ - Ursell factors. Collapsed series of activities for 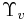$~\Upsilon_v$ we obtain the alternative representation

$~\Upsilon_v = \exp{\beta [ vP(z,T) %2B a\sigma (z,T) ]},$

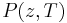where $~P(z,T)$ is the pressure, 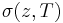$~\sigma (z,T)$ - coefficient of surface tension on the interface of the fluid and hard solid, 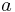$~a$ - the surface bounding the system.

It should be stressed that an open system does not singled out, and the surface tension is created due to the fluctuation component of the partition function.

The last expression is exactly consistent with the probability of the formation of the hole volume 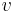$~v$ in the fluid

$~p^v_0 = \exp-{\beta [ vP(z,T) %2B a\sigma (z,T) ]},$

is determined from thermodynamic considerations

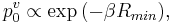
$~p^v_0 \propto \exp{( -\beta R_{min})},$

where 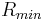$~R_{min}$ - minimum work of formation of such fluctuations.

Some properties of the OSE

Scale invariance. In contrast to grand canonical ensemble, an open statistical ensemble satisfies the scale invariance requirement: general term of the included subsystem distribution corresponds to that of the original system.

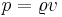Application to small systems. This distribution may be applied to however small volumes including those less than a molecule size. In this case it degenerates into a Bernoulli distribution with $~p=\varrho v$ .

Separation of fluctuations. When volume is much greater than the size of the molecule squared deviation of the number of particles is divided into bulk and surface terms.

References

Zaskulnikov V. M., Open statistical ensemble and surface phenomena: arXiv:0911.3106
Zaskulnikov V. M., Open statistical ensemble: new properties (scale invariance, application to small systems, meaning of surface particles, etc.): arXiv:1004.0896v1

Statistical mechanics

Statistical ensembles	Microcanonical • Canonical • Grand canonical • Isothermal–isobaric • Isoenthalpic–isobaric • Open

Statistical thermodynamics	Characteristic state functions

Partition functions	Translational • Vibrational • Rotational

Equations of state	Dieterici • Van der Waals • Ideal gas law • Birch–Murnaghan

Entropy	Sackur–Tetrode equation • Tsallis entropy

Particle statistics	Maxwell–Boltzmann statistics • Fermi–Dirac statistics • Bose–Einstein statistics

Statistical field theory	Conformal field theory • Osterwalder–Schrader axioms

See also	Probability distribution • Structureless particles